常用的等离子体数值模拟方法包括粒子方法和流体方法。前者结果精确,但需求较高的计算资源,不适用于大尺度、高密度等离子体;流体方法便于研究大范围、长时间等离子体性质,但不能准确捕获局部粒子动力学特性。 为了兼顾计算的准确性和效率,等离子体混合模型(Hybrid model)受到越来越多的重视。本期速读一篇基于三维混合代码研究真空电弧熄弧过程的佳作:[1] Cao Z, Wang Z, Chen F, et al. "3D Hybrid Modelling of Extinction of Multiple Cathode Spots in Vacuum." Journal of Physics D: Applied Physics 53(2020):405202.
真空电弧本质是一种由离散的阴极斑点所发射的等离子体射流,典型的熄弧过程如下图所示: (1)阴极斑点喷射出的离子动能为40~60eV,而温度仅0.5~1.5eV,体现出很强的粒子特性; (2)电子热速度要远大于其漂移速度,体现出气体特性; (3)熄弧过程中,电流从峰值迅速衰减到零,阴极斑点的数目随着电流的降低而逐渐减少,粒子密度在熄弧过程中跨越多个数量级。 由于兼具粒子与流体属性,且计算粒子数密度数量级变化巨大,单纯的流体/粒子方法均无法满足模拟需求。 文章采用了混合模拟方法:将离子处理为宏粒子,使用粒子方法追踪其在自生电磁场和外部场中的运动,电子则被考虑为无质量流体[1],从而在节省计算资源的基础上,保留了全部离子动力学行为,并且可以方便地考虑多种离子种类问题[2]。为了考虑离散阴极斑点在熄弧过程中的不对称性,采用三维模型进行仿真,模型设置如下图所示。 式中ne、me、ve和e分别代表电子数密度、电子质量、电子速度和电子电荷;Pe是电子压力;j是电流密度;σ是等离子体电导率;E和B分别为电场强度和磁感应强度。(1)式等号右边的最后一项代表电子和离子之间碰撞阻力的影响[1]。 电子和离子之间的碰撞频率、等离子体电导率为[3,4]: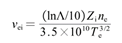
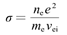
离子作为宏粒子考虑,其位移由运动方程决定,加速度由洛伦兹力决定[5]: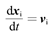
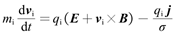
式中mi、xi、qi和vi分别代表离子质量、离子位移、离子电荷和离子速度。洛伦兹力方程等号右边的最后一项和电子动量方程式中的对应项平衡。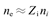
电子和离子是电流的载体,电流密度与电子和离子运动速度之间的关系为:
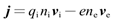
电流密度由安培环路定律给出,其中位移电流项被忽略(达尔文静磁近似):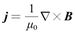
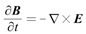
代码推进采用了蛙跳格式,将粒子的位置和速度分别存储在相差半个时间步长的时间节点上。在每个推进步内,首先推动粒子的位置。然后在Yee氏交错网格上,使用时域有限差分法计算电磁场。最后使用Boris算法追踪粒子在电磁场中的运动。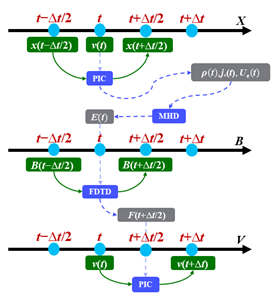
图3 时间步推进示意图 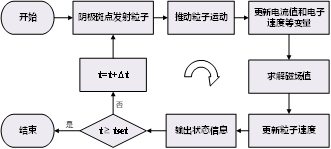
图4 程序执行步骤 下图给出了熄弧过程中离子数密度分布。等离子体射流从阴极斑点产生,并逐渐汇合形成等离子体通道。随着阴极斑点熄灭,阴极表面的离子密度分布变得不对称。 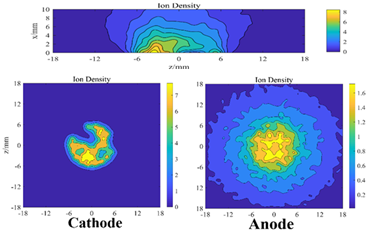
图5 熄弧过程中的离子数密度分布 下图给出了不同切断时间下,电流零点时刻附近的离子密度分布的变化过程,以及极间剩余离子数和离子平均速度随时间的变化曲线。由图可知,电流的切断时间决定了阴极斑点的熄灭速率。切断时间越短,则离子密度分布受已熄灭的阴极斑点的影响越大,并且电流零点时刻的剩余离子数越多,离子迁移速度越低。
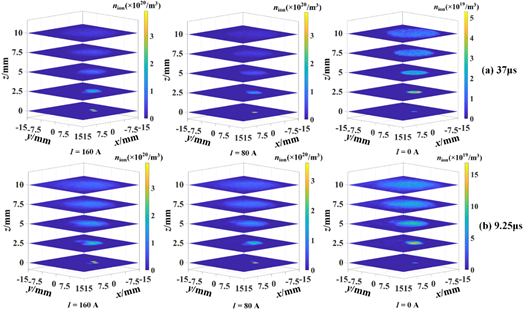
图6 不同切断时间下,电流零点时刻附近的离子密度分布的变化过程 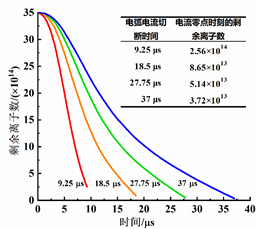
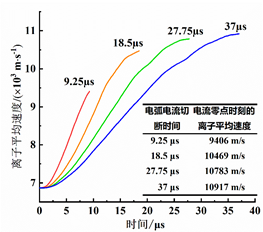
图7 极间剩余离子数和离子平均速度随时间的变化曲线 当阴极表面仅剩余三个阴极斑点时,考虑两种极端情况:彼此相距最近(近态)和相距最远(远态)。下图给出了在电流零点时刻,两种情况下最后熄灭的阴极斑点所在垂线上的离子密度曲线。可以看出,阴极斑点位置分布对于局部离子密度分布有较大影响。两种情况下局部离子数密度的最大值相等,但在最大值之后,近态下的局部离子数密度要高于远态。
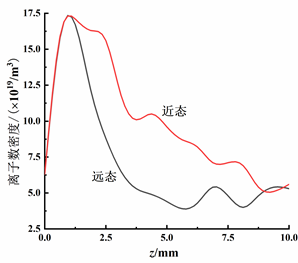
图8 电流零点时刻,两种情况下最后熄灭的阴极斑点所在垂线上的离子密度曲线 参考文献 [1] D. Winske and N. Omidi, Hybrid codes: Methods and applications. Los Alamos National Lab., NM (USA), 1991. [2] C. Li, U. Ebert, and W. Hundsdorfer, "Spatially hybrid computations for streamer discharges with generic features of pulled fronts: I. Planar fronts," Journal of Computational Physics, vol. 229, no. 1, pp. 200-220, 2010. [3] S. Braginskii and M. Leontovich, "Reviews of plasma physics," ed: Consultants Bureau New York, 1965. [4] I. Beilis, M. Keidar, R. Boxman, and S. Goldsmith, "Theoretical study of plasma 
喜欢请关注公众号:等离子体计算工坊

公众号交流微信:工坊君
你感兴趣的就是工坊希望和你共同学习的 |